Gerak Lurus Berubah Beraturan

Gerak lurus berubah beraturan adalah gerak yang lintasannya berupa garis lurus dengan kecepatannya yang berubah beraturan.

Percepatannya bernilai konstan/tetap.

Rumus GLBB ada 3, yaitu:

• ${\displaystyle \!v_{t}=\!v_{0}+\!a\times \!t}$

• ${\displaystyle \!s=\!v_{0}\times \!t+{\frac {1}{2}}\times \!a\times \!t^{2}}$

• ${\displaystyle \!v_{t}^{2}=\!v_{0}^{2}+\!2\times \!a\times \!s}$

Dengan ketentuan:

• ${\displaystyle \!v_{0}}$ = Kecepatan awal (m/s)
• ${\displaystyle \!v_{t}}$ = Kecepatan akhir (m/s)
• ${\displaystyle \!a}$ = Percepatan (m/s²)
• ${\displaystyle \!s}$ = Jarak yang ditempuh (m)

Gerak vertikal ke atas

Benda dilemparkan secara vertikal, tegak lurus terhadap bidang horizontal ke atas dengan kecepatan awal tertentu. Arah gerak benda dan arah percepatan gravitasi berlawanan, gerak lurus berubah beraturan diperlambat.

Peluru akan mencapai titik tertinggi apabila V_t sama dengan nol.

${\displaystyle t_{\text{maks}}={\frac {Vo}{g}}}$

${\displaystyle h={\frac {Vo^{2}}{2g}}}$

${\displaystyle t={2}\times {t_{\text{maks}}}}$

${\displaystyle {V_{\text{t}}^{2}}=V_{\text{0}}^{2}-2\times {g}\times {h}}$

Keterangan:

• Kecepatan awal= Vo
• Kecepatan benda di suatu ketinggian tertentu= Vt
• Percepatan /Gravitasi bumi: g
• Tinggi maksimum: h
• Waktu benda mencapai titik tertinggi: t _maks
• Waktu ketika benda kembali ke tanah: t

Gerak jatuh bebas

Benda dikatakan jatuh bebas apabila benda:

• Memiliki ketinggian tertentu (h) dari atas tanah.
• Benda tersebut dijatuhkan tegak lurus bidang horizontal tanpa kecepatan awal.

Selama bergerak ke bawah, benda dipengaruhi oleh percepatan gravitasi bumi (g) dan arah kecepatan/gerak benda searah, merupakan gerak lurus berubah beraturan dipercepat.

${\displaystyle v={\sqrt {2gh}}}$

${\displaystyle t={\sqrt {2h/g}}}$

Keterangan:

• v = kecepatan di permukaan tanah
• g = gravitasi bumi
• h = tinggi dari permukaan tanah
• t = lama benda sampai di tanah

Gerak vertikal ke bawah

Benda dilemparkan tegak lurus bidang horizontal arahnya ke bawah.

Arah percepatan gravitasi dan arah gerak benda searah, merupakan gerak lurus berubah beraturan dipercepat.

${\displaystyle Vt={Vo}+g\times t}$

${\displaystyle Vt^{2}={Vo^{2}}+2\times g\times h}$

Keterangan:

• Vo = kecepatan awal
• Vt = kecepatan pada ketinggian tertentu dari tanah
• g = gravitasi bumi
• h = jarak yang telah ditempuh secara vertikal
• t = waktu

Sumber : https://id.wikibooks.org/wiki/Rumus-Rumus_Fisika_Lengkap/Gerak

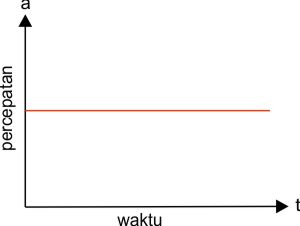
Grafik Percepatan terhadap Waktu

Gerak lurus berubah beraturan (GLBB) adalah gerak lurus dengan percepatan tetap. Dengan demikian grafik hubungan percepatan dengan waktu adalah seperti garis horisontal yang sejajar dengan sumbu x. Mau di detik berapun percepatan yang dialamai oleh beda yang melakukan GLBB adalah tetap. Berikut gambar grafiknya

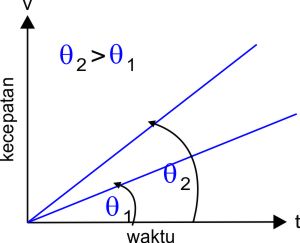
Grafik Kecepatan terhadap Waktu

Bentuk grafik hubungan antara kecepatan dan waktu adalah seperti persamaan garis lurus. Grafik tersebut memiliki kemiringan (gradien) tertentu. Coba sobat amati grafik di atas. Grafik hubungan V dan t jika kecepatan awal(Vo) adalah nol ditunjukkan oleh grafik a dan jika kecepatannya adalah Vo maka grafiknya seperti tampak pada grafik b.

Dari grafik di atas bisa sobat amati adanya kemiringan (gradien garis). Pada prinsipnya rumus kecepatan pada GLBB Vt = Vo + at  sama seperti rumus pada persamaan garis lurus y = mx + c. Vt dianalogikan dengan y, c dianalogikan dengan kecepatan awal Vo, dan mx dianalogikan dengan at. Besarnya percepatan a akan sama dengan kemiringan garis (gradien). Rumusnya

a = tan θ

Jadi, pada gerak lurus berubah beraturan kemiringan grafik hubungan v dengan t adalah sama dengan percepatan yang terjadi pada gerak tersebut. Semakin curam grafik tersebut maka semakin besar percepatannya. Dengan melihat ilustrasi di bawah ini sobat bisa tahu bahwa grafik a yang lebih curam punya percepatan yang lebih besar dari grafik b yang bentuknya lebih landai.

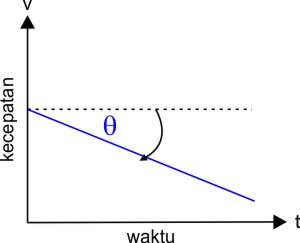
Untuk grafik hubungan v dan t yang bergerak dari kiri bawah ke kanan atas maka nilai percepatannya adalah positif yang berarti GLBB dipercepat. Akan tetapi ada juga grafik hubungan v dan t yang bergerak dari kiri atas ke kanan bawah, yaitu untuk GLBB diperlambat dengan nilai percepatan negatif.  Simak grafiknya berikut

 

Grafi Hubungan Jarak (kedudukan) dengan Waktu

Grafik terakhir dalam GLBB adalah hubungan antara jarak atau kedudukan terhadap waktu. Saat kita belajar GLBB kita tahu persamaan untuk mencari jarak adalah

x = xo + vot + 1/2at2

Jika sobat lihat dari persamaan di atas jaraka (x) adalah fungsi kuadrat dari waktu (t). Seperti yang kita pelajari tentan fungsi kuadrat, grafik fungsi kuadrat berbentuk parabola. Berikut kemungkinan grafik hubungan x dengan t pada gerak lurus berubah beraturan.

Grafik	Keterangan
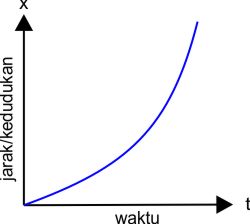	Grafik dengan percepatan positif (a>0) berbentuk parabola terbuka ke atas dengan kecepatan awal Vo dan kedudukan awal xo = 0
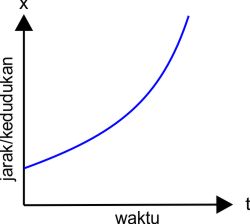	Grafik dengan percepatan positif (a>0) berbentuk parabola terbuka ke atas dengan kecepatan awal Vo dan kedudukan awal xo ≠ 0
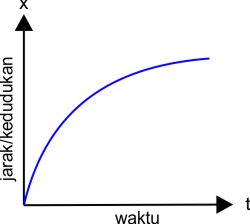	Grafik dengan percepatan negatif (a<0) berbentuk parabola terbuka ke atas dengan kecepatan awal Vo dan kedudukan awal xo = 0
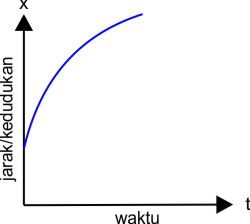	Grafik dengan percepatan negatif (a<0) berbentuk parabola terbuka ke atas dengan kecepatan awal Vo dan kedudukan awal xo ≠ 0

Sumber : http://rumushitung.com/2014/04/07/grafik-gerak-lurus-berubah-beraturan-glbb/